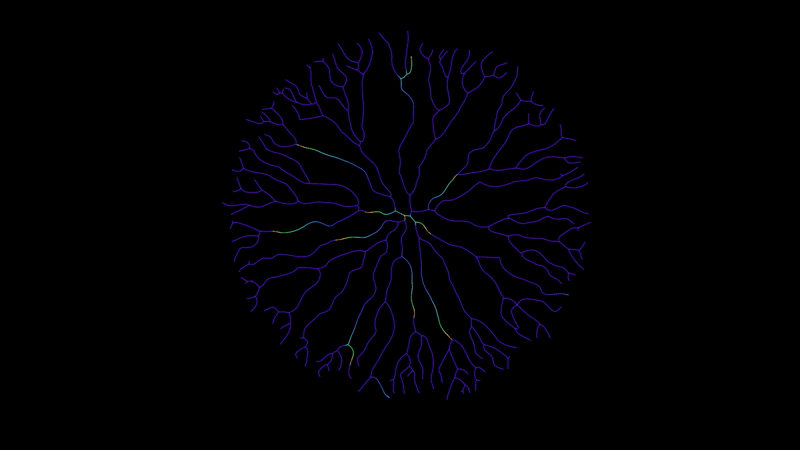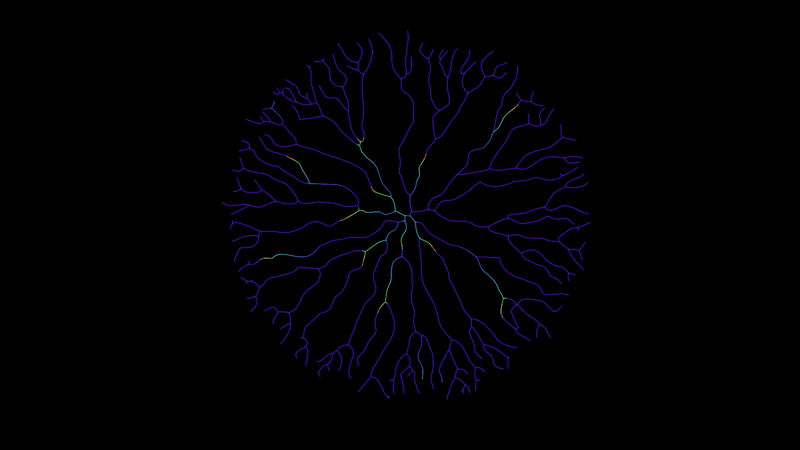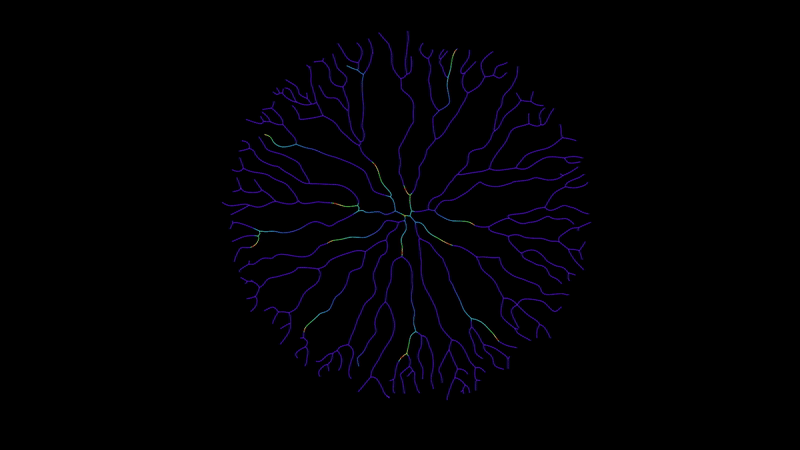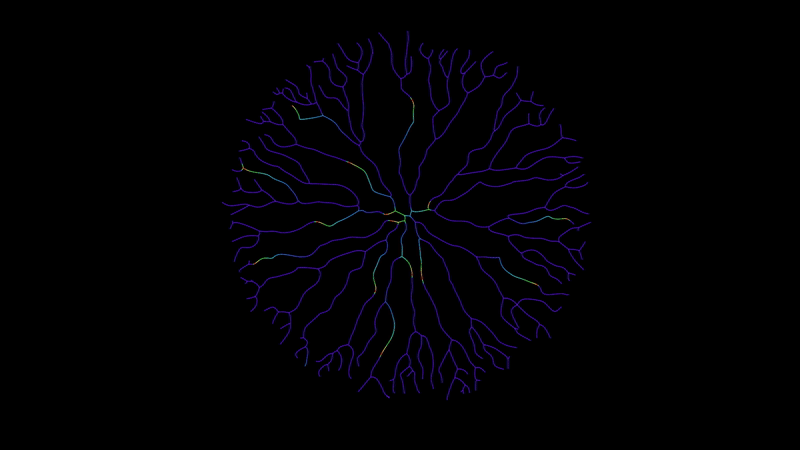
This example starts with a 2D curve network.

The input to the FindShortestPathSOP is created via a circleSOP and then a VoronoiFractureSOP, with a bias favouring end points further away from the origin to give smaller tips to the longer main branches.

Beyond the typical cleanup (SubdivideSop, FuseSOP, PolyPathSOP…) we need a few things before we feed the network into a SolverSOP:

The crux of the effect relies on activating points based on their connected neighbours. With every step, we define points next to the leading edge of an energy pulse, fill them with energy, and then we use these new leading points to activate the leaders in the next step. Rinse and repeat.

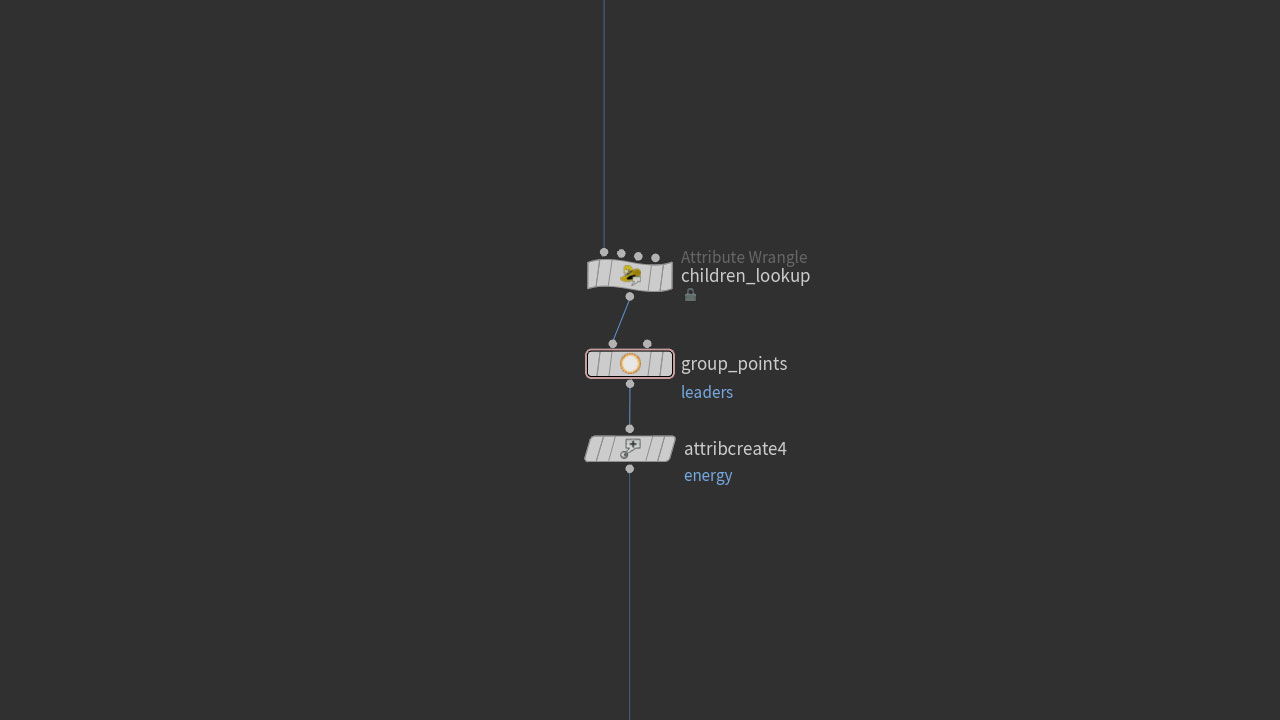
So we need a “leaders” group that contains our root point 0 (as with other examples, the network has a single root). We also create an attribute to contain the energy, and set the energy of the leading group to 1.0.

The final piece of setup is the creation of an array attrib to hold all of a point’s downstream connections. Best to do this before animation begins so that we’re not continiually recomputing values that never change. Instead, let’s store them for a simple lookup later on:

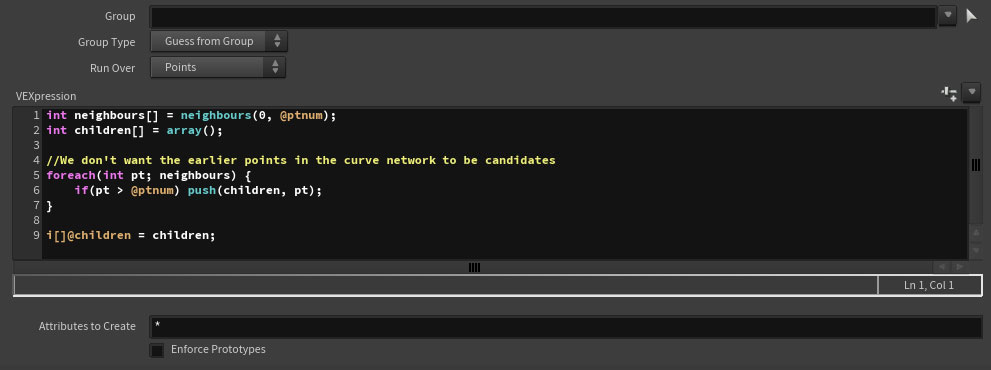
The general principle is that we’re defining a set of subsequent points that each point can pass energy to. We use connectivity information here, but many other relationships exist. I’ve also had interesting results when defining a “Look At” vector with a cone angle to identify neighbours, useful for points that are not geometrically connected.

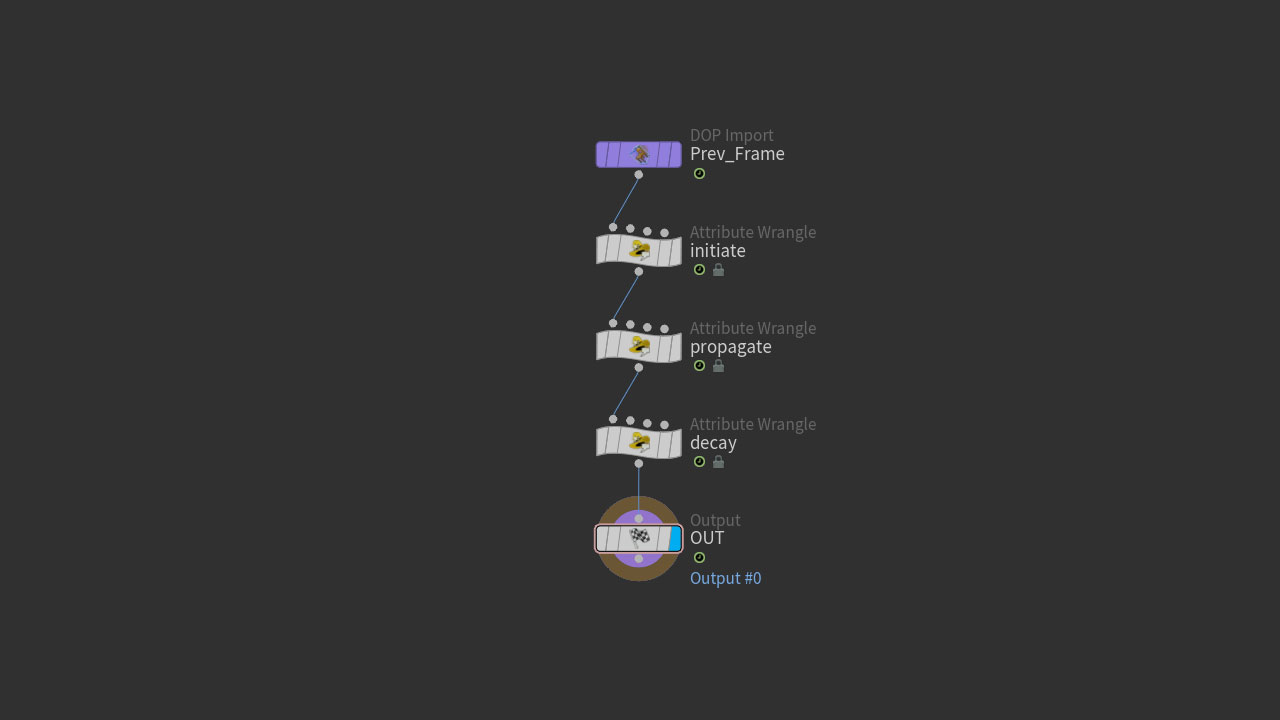
Next, a solver with three simple steps:

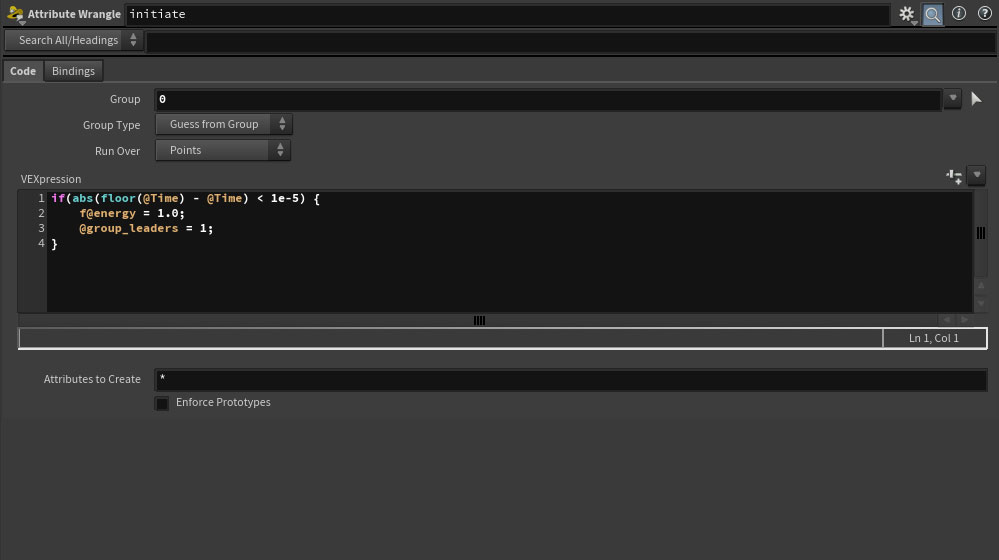
Step 1. Once every second, add our root point to the leaders group and give it an energy of 1.0:

Step 2. For every leader, pick the first point in that leader’s children array (the lookup we created earlier). Make the selected child point a leader, and give it an energy value of 1.0. We then move the energized child to the end of the array (this has no effect on points with only a single child). We could also pick children at random, but I liked the result of cycling through the array that we see at the top of the page. With the leader’s work complete, we remove it from the leaders group.

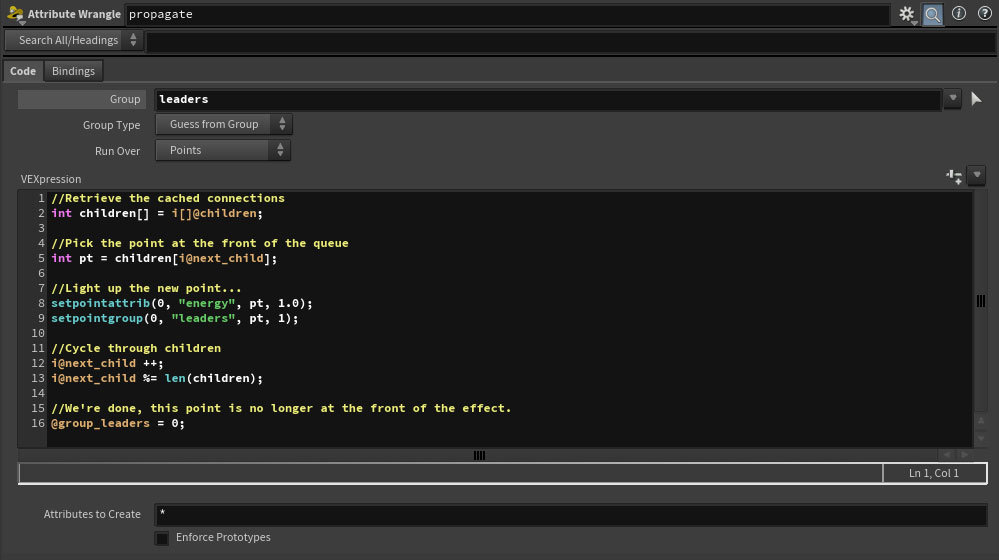
Step 3. Finally, we multiply down the energy to fade it out over time.

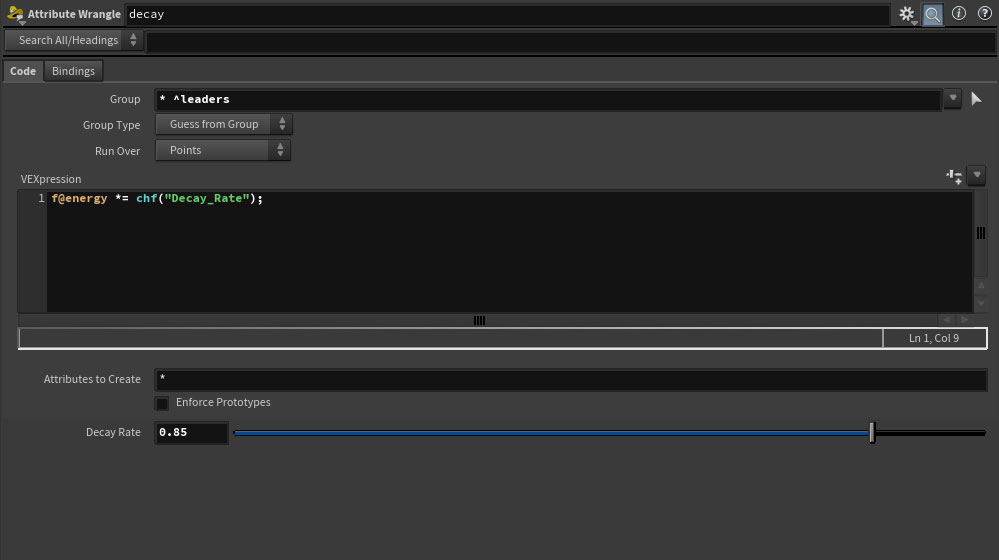
One limition of this setup is that the speed of traversal relies on the density of points on a prim. A hasty way to increase the speed of animation would be to loop through the Solver more than once, like this:

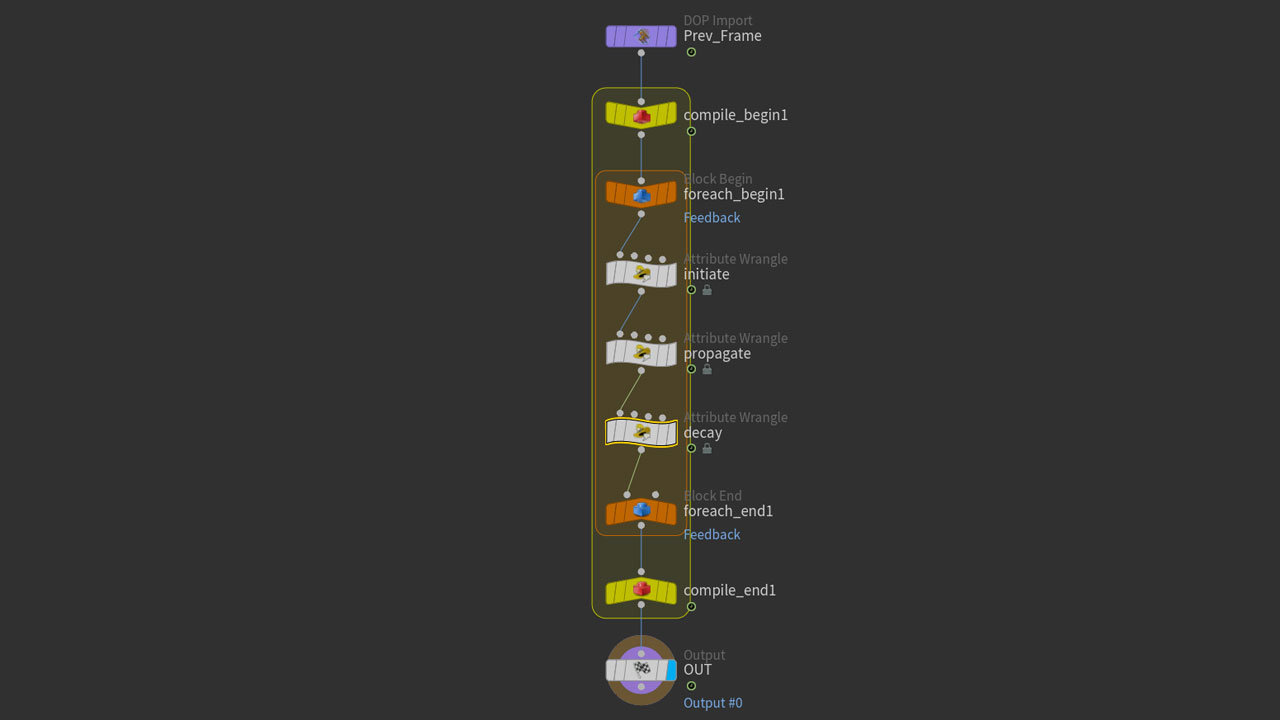
The last thing would be to inspect the energy attrib outside of the solver watch a nice flow of energy over the network, radiating out from the root.