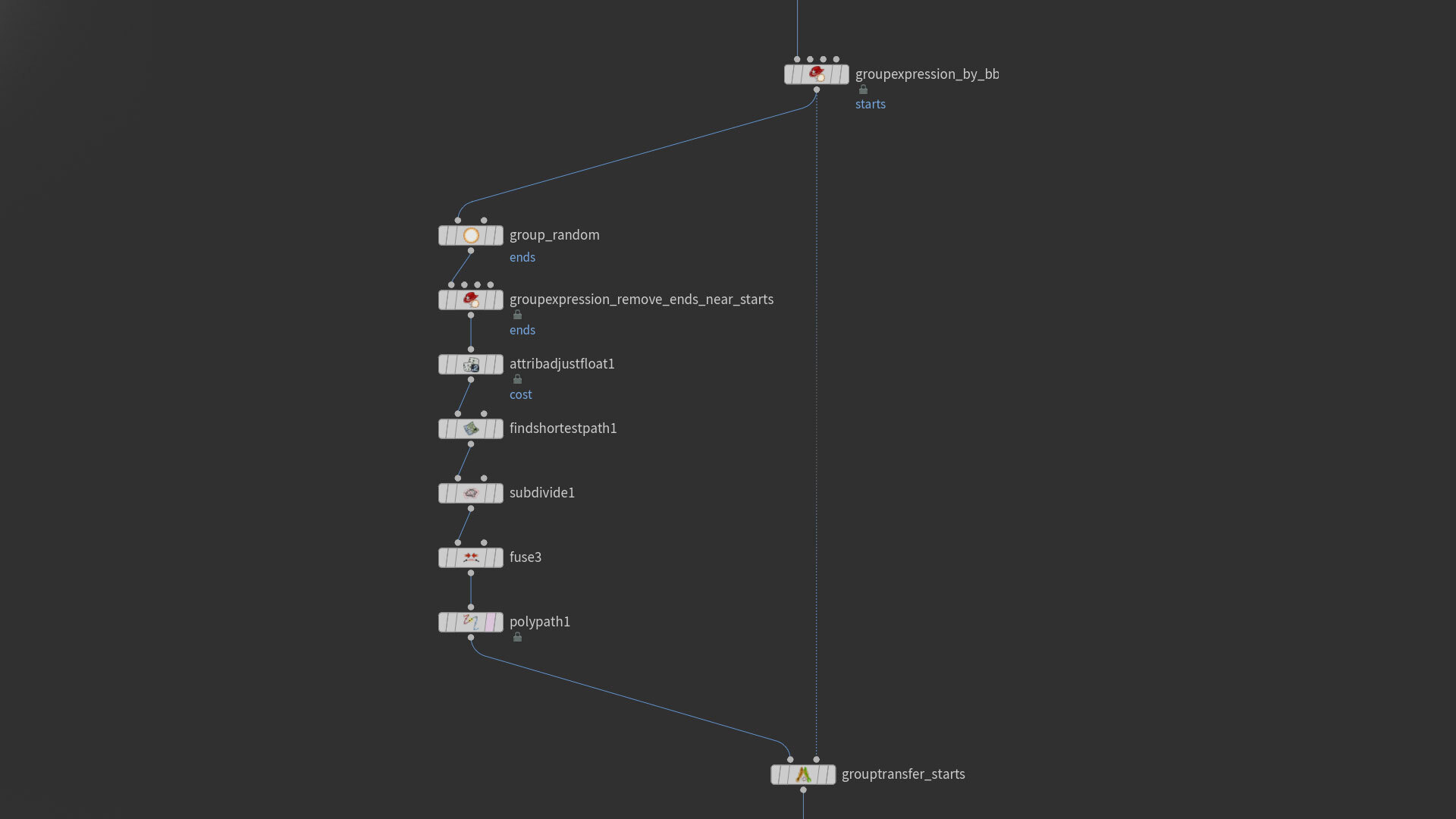
Surface growth
Another day, another tendril setup.

The input geo here starts with a grid of squares, with each square then scaled down to their centroids via the ExtrudeSOP, followed by a FuseSOP to remove subsequently overlapping points. Essentially this, but at a suitably high resolution:
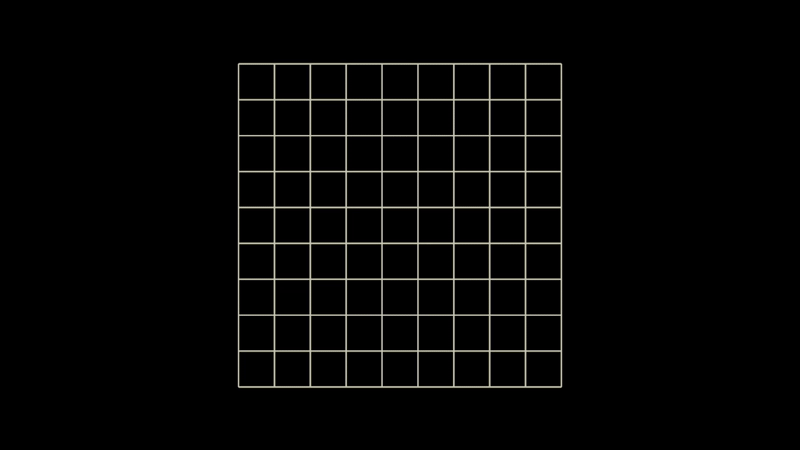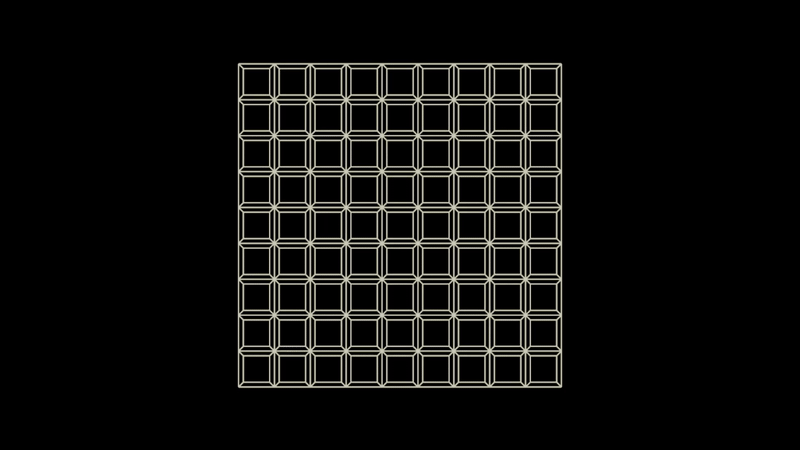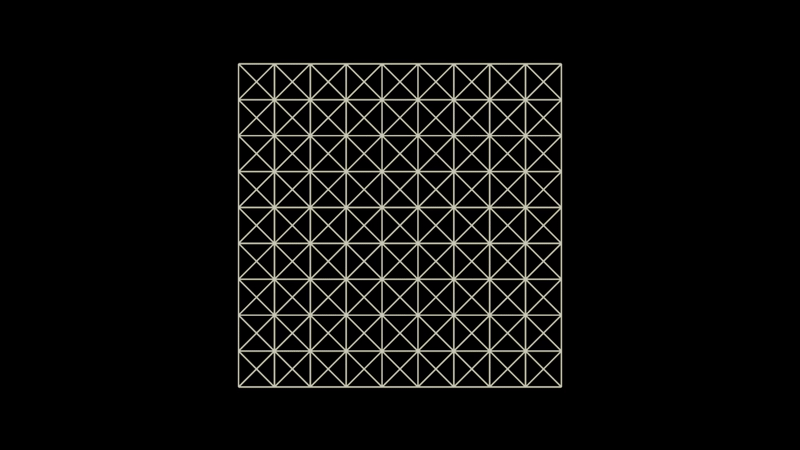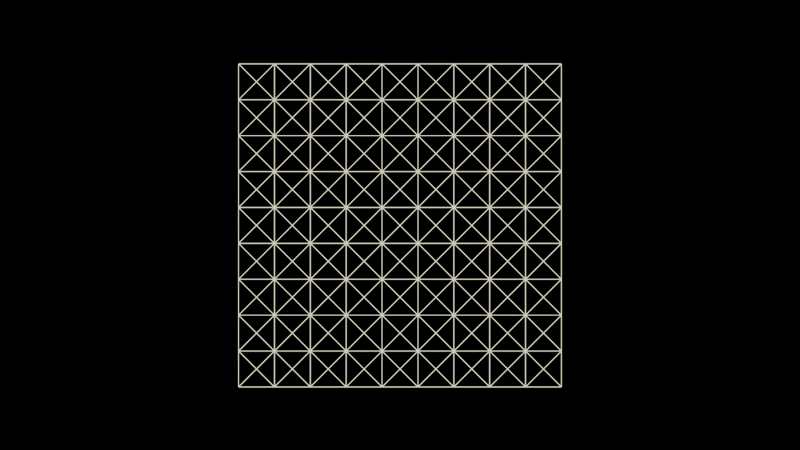
We want all the FSP start points from along one open edge of the input grid. This VEX in a point wrangle will do that:
@group_starts = relpointbbox(0, @P).y == 0.0
We then select end points randomly with a GroupSOP. Typical stuff. As a final step, from the end group we remove points that are too close to the starting line with a second point wrangle/ bounding box function:
@group_ends *= relpointbbox(0, @P).y > 0.6
The next few steps are extremely similar to this example (and others - these are extremely common techniques)…
We subdivide the curves and use the typical combination of a FuseSOP followed by a PolyPathSOP to convert the mass of overlapping prims into a tidy curve network.

We also need an accumulating arrival time attrib beginning at our start points. For that we need our start group, but this will have been destroyed by the FSP operation. With many points in the FSP start group network it’s worth restoring that group procedurally.
The last few operations will look a bit like this:
Now, to animate. As in this example we carve by our accumulating attrib and, hey presto, animated growth. However, the result feels very linear, which becomes jarring where the animation comes to an abrupt stop at the terminal prims.

To grade the animation we can adjust arrival time attrib, stretching and compressing time to affect the speed at which things occur. Larger ranges of arrival time along a prim will slow animation (and vice versa), while non-linear adjust will create non-linear animation (easing).
SO. We first need to isolate the terminal prims. We can find them by identifying terminal points with this in a point wrangle:
@group_tips = neighbourcount(0, @ptnum) == 1 && !inpointgroup(0, "starts", @ptnum)
We that feed the resulting point group into a GroupPrommoteSOP to prims. After that it’s a straightforward case of adding to the original arrival time over the length of the prim, with a chramp parm to introduce non-linearity.
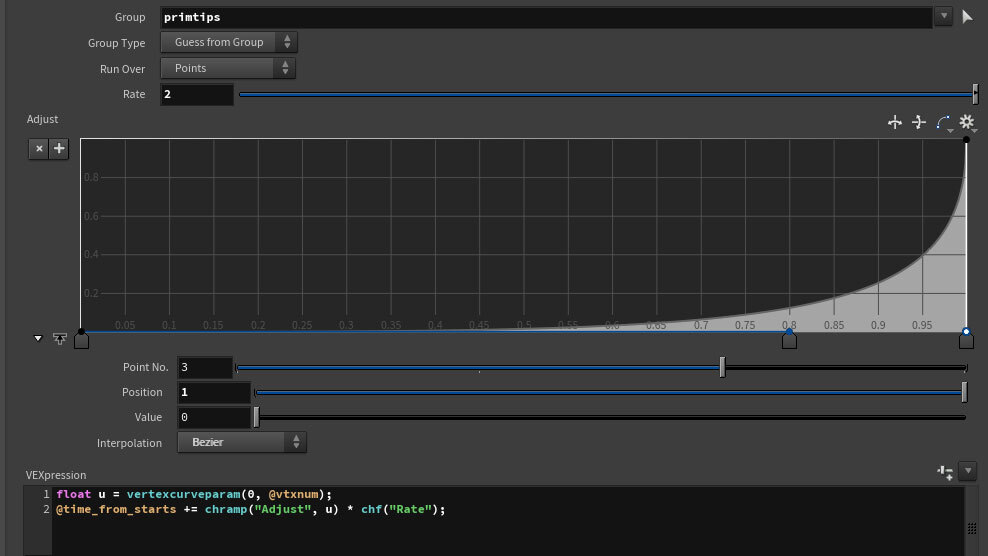
The result of this adjustment is the terminal prims slowing to a stop as the wandering tendrils arrive at their destinations (the slightly staccato GIF does us no favours here, but rest assured it’s smoother :)):

What remains is to scatter points on the pre-carved curved network, and then either AttribInterpolateSOP the animated values to those points to drive colour and scale, or perhaps measure the distance between the scattered points and the carved curve network - the greater the distance from the curve network, the less active the points will be.
For the larger circles on the ends of the terminal prims, we need to know the ratio of prim length pre and post carve, a value that will increase from 0.0 to 1.0 as the length of a prim arrives at its pre-carve state.